A Remarkable Sequence in OEIS

The On-Line Encyclopedia of Integer Sequences (OEIS), launched in 1996, now contains 360,000 entries. It attracts a million visits a day, and has been cited about 10,000 times. It is now possible for anyone in the world to propose a new sequence for inclusion in OEIS. The goal of the database is to include all interesting sequences of integers. The present growth rate is about 12,000 new entries each year.

The main applications of the database are in identifying sequences and in finding out the current status of a known sequence. Mathematical writer Barry Cipra has described OEIS as the mathematical analogue of a “fingerprint database”. There is a wealth of interesting material on OEIS. We examine here a particular and remarkable sequence, Recamán’s Sequence (A005132), which has resisted analysis for over 30 years.

Recamán‘s Sequence (A005132)

Named for its inventor, Colombian mathematician Bernardo Recamán Santos, the Recamán sequence is defined by the recurrence relation

$\displaystyle a_n = \begin{cases} 0 & n = 0 \\ a_{n-1}-n & a_{n-1}-n >0 \text{, not already in sequence} \\ a_{n-1}+n & \text{ otherwise} \end{cases}$

Thus, we start with ${a_0=0}$ and, for each ${n}$ in turn, we subtract ${n}$ if this produces an unused positive number, or else add ${n}$ for the next term. So, from 0 we get 1, then add 2 to get 3, add 3 to get 6, subtract 4 to get 2, and so on. The big unanswered question is this:

Does the sequence contain every number?

The sequence is not a permutation of the integers: some values are repeated, the first being ${a_{20} = a_{24} = 42}$ . The terms satisfy ${a_n\ge 0}$ and ${| a_{n}-a_{n-1} | = n}$ for all ${n}$ . The number 4 does not occur until step 131. The first 50 terms of the sequence are

0, 1, 3, 6, 2, 7, 13, 20, 12, 21, 11, 22, 10, 23, 9, 24, 8, 25, 43, 62, 42,

63, 41, 18, 42, 17, 43, 16, 44, 15, 45, 14, 46, 79, 113, 78, 114, 77,

39, 78, 38, 79, 37, 80, 36, 81, 35, 82, 34, 83, …

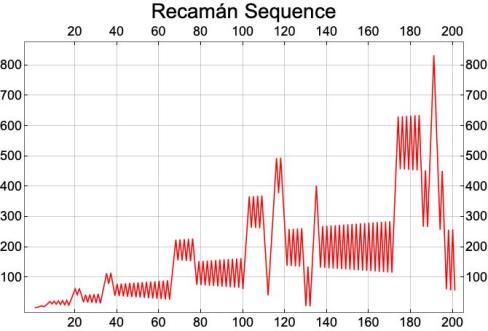
A graph of the first 200 terms of Recamán’s Sequence is shown in the Figure above. On the OEIS website, it is possible to click a button “listen”, which generates an acoustic signal from the sequence. Recamán’s sequence produces an extraordinary signal, which has aspects of a human-produced avant-garde musical composition.

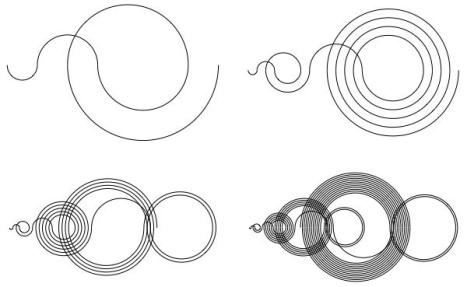
Recamán’s sequence as pictured by Edmund Harriss. Upper left: 5 terms. Upper right: 15 terms. Lower left: 30 terms. Lower right: 60 terms.

Neil Sloane (2023) discussed Recamán’s Sequence in some detail. He described the method of illustrating the sequence, devised by Edmund Harriss, who depicts the terms in an elegant way, as a spiral on the number line (figure above). It starts at 0, the point at the extreme left. If ${n}$ is subtracted, we draw a semicircle of diameter ${n}$ to the left from the previous point. If ${n}$ is added, we a draw a semicircle of diameter ${n}$ to the right. The semicircles are drawn alternately below and above the horizontal axis in order to produce a smooth ( ${C^1}$ ) spiral. In the figure, spirals are shown for ${n\in\{5, 15, 30, 60\}}$ .

Summary of OEIS

An excellent review of OEIS has just appeared in the journal Mathematical Intelligencer. The author Neil Sloane, who started the entire venture, summarises the database in a list of bullets, including the following:

Accurate information about 360,000 sequences.
Definition, formulas, references, links, programs.
Results viewable as a list, table, graph or audible as music!
Site traffic is approximately 1 million hits a day.
There are 30 new entries, 50 updates every day.
Site has been called a fingerprint database for mathematics.
It has about 10,000 academic citations.
There are both very easy and very hard problems: “Catalan or Collatz”.
A source of fascinating research problems
Results are accessible and freely available.
Great educational benefits. Has attracted many people into mathematics.
One of the most successful international collaborations,

Sloane also points out that the project needs more voluntary editors. If you are interested, contact the OEIS Foundation.

That’s Maths has posted an article on OEIS (link). To investigate or search for a sequence, you simply enter the first few terms of the sequence into the search field on the OEIS home page. If the sequence is in the database, the response will give a definition of the first 50 or so terms, and much information about the sequence.

Sources

${\bullet}$ Sloane, N. J. A., 2023: The Mathematical Intelligencer, 45(3), 193–205. PDF:

${\bullet}$ OEIS Official Website: https://oeis.org/

${\bullet}$ That’s Maths post on OEIS. Link.

Related

Published by thatsmaths