Pythagorean Tuning and the Spiral of Theodorus

The notes of the chromatic scale in the key of C.

Most of us are familiar with the piano keyboard. There are twelve distinct notes in each octave, or thirteen if we include the note completing the chromatic scale. The illustration above shows a complete scale from middle C (or C ${_4}$ ) to the C above (or C ${_5}$ ). Eight of the notes — C, D, E, F, G, A, B and another C one octave higher — comprise the `diatonic scale’, while the remaining five sharp notes (denoted ${\sharp}$ ) complete the chromatic scale.

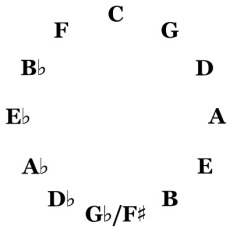The piano keyboard makes no distinction between C ${\sharp}$ and D ${\flat}$ : both are sounded by pressing the same key. But there is a difference: in some tuning methods, the two notes are slightly different in pitch. Instruments like the violin, with continuous pitch rather than discrete notes, can resolve the distinction, which is known as enharmony. We can illustrate it by constructing the “Circle of Fifths”.

In Pythagorean tuning, the octave is made up by repeated formation of Perfect Fifths, in which each successive note has a frequency ${\frac{3}{2}}$ times the previous one. The frequency is halved where necessary to keep within the range of a single octave, let’s say, between C ${_4}$ and ${C_5}$ .

Moving up an interval of a fifth, we go from C to G. Repeating, we get in turn D, A, E, B and F ${\sharp}$ . This involves six factors of ${\frac{3}{2}}$ and three factors of ${\frac{1}{2}}$ to keep within C ${_4}$ — ${C_5}$ . Thus, the pitch of F ${\sharp}$ is ${3^6/2^9}$ above C.

Now drop down from C by a fifth to F, then to B ${\flat}$ , E ${\flat}$ , A ${\flat}$ , D ${\flat}$ and G ${\flat}$ . This gives six factors of ${\frac{2}{3}}$ and four factors of ${{2}}$ to keep within C ${_4}$ — ${C_5}$ . Thus, the pitch of G ${\flat}$ is ${2^{10}/3^6}$ above C. So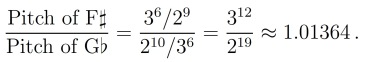This number is called the Pythagorean Comma.

Another way to look at this is to consider a series of twelve notes, each a perfect fifth above the preceding one. Allowing for the reduction to the same octave, we start at Middle C and end at a note whose frequency differs from Middle C by a factor equal to the Pythagorean Comma.

Geometric Construction

Fig. 1. Left: Triangle for a perfect fourth. The perpendicular drawn from C cuts the frequency axis at a point that is 4/3 times the distance AB, a perfect fourth. Right: Triangle for constructing perfect fifths.

Three Norwegian authors, Börre Nyhoff, Alv Aarskog and Sverre Holm (2024), have recently published a paper in the Mathematical Intelligencer, in which they present a geometric construction of musical scales and illustrate the Pythagorean Comma.

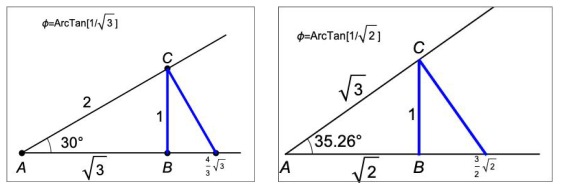
The aim is to arrange the notes of the scale on a line — the frequency axis — using simply geometry to obtain the required frequency ratios. We start with a right-angled triangle. If the side lengths are 1, ${\sqrt{3}}$ and 2, the angle A is ${30^\circ}$ , as in Fig. 1 (left panel), and the perpendicular drawn from C cuts the frequency axis at a point that is ${\frac{4}{3}}$ times the distance AB. This ratio corresponds to a musical interval of a fourth.

If the angle ${30^\circ}$ is replaced by ${\arctan 1/\sqrt{2} = 35.26^\circ}$ , the ratio ${\frac{4}{3}}$ is replaced by ${\frac{3}{2}}$ , corresponding to a perfect fifth (Fig. 1, right panel).

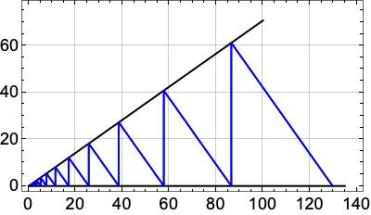
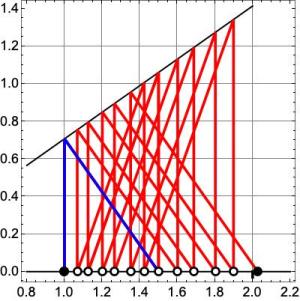
Fig. 2. Pythagorean tuning with ascending fifths not confined to a single octave

Fig. 3. Pythagorean tuning of complete chromatic scale constructed with ascending fifths. The final note has pitch slightly more than twice the base note.

Repeating this construction, we can produce the complete chromatic scale. Fig. 2 shows a sequence of twelve ascending fifths. The ratio of the last note to the first is ${(3/2)^{12} = 129.74}$ , corresponding closely to ${2^7 = 128}$ , or seven octaves. The ratio ${129.74/128 = 1.0136}$ , the Pythagorean Comma.

Fig. 3 shows the full chromatic scale, with octave equivalence where pitches are halved or doubled to remain within a single octave (except for the final C). We can see that this final C has a pitch slightly above C ${_5}$ , the discrepancy being the Pythagorean Comma.

The Spiral of Theodorus

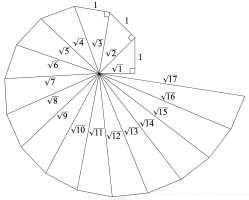
The triangles appearing in Fig. 2 are special cases of the infinite sequence of right-angled triangles used to construct the Spiral of Theodorus (ThatsMaths, 2021). Starting with the isosceles triangle having sides ${\{1,1,\sqrt{2}\}}$ we adjoin triangles of sides ${\{1,\sqrt{n},\sqrt{n+1}\}}$ (see Fig. 4). The smallest angle of the ${n}$ -th triangle is ${\arctan 1/\sqrt{n}}$ and the tuning ratio is ${\frac{n+1}{n}}$ . Thus, we can construct musical scales by using series of notes with any interval ${(n+1)/{n}}$ .

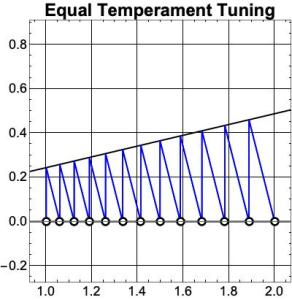
A sequence of perfect fifths can never produce two notes with an octave interval: no ratio of the form ${3^m/2^n}$ is a whole number, because ${3^m}$ is odd and ${2^n}$ even. To have an octave of thirteen notes with each adjacent pair having the same frequency ratio, ${r}$ , we would need the product of ${r}$ by itself twelve times to equal 2. Therefore, ${r = \sqrt[12]{2} \approx 1.06}$ . Such a tuning scheme is called equal temperament. It has many advantages, but involves a compromise: notes separated by a fifth have frequency ratio ${r^7 \approx 1.498}$ instead of the perfect value ${1.5}$ . All the other intervals are also irrational so that only octaves (eighths) have the ideal ratio ( ${2:1}$ ). Fig. 5 shows an octave tuned with equal temperament: the thirteenth note is exactly C ${_5}$ .

Fig. 5. An octave tuned with equal temperament.

Sources

${\bullet}$ Nyhoff, Börre, Alv I. Aarskog and Sverre Holm, 2024: Geometric Construction of Pythagorean and Just Musical Scales and Commas. Math. Intelligencer, 46, 25–31.

${\bullet}$ ThatsMaths, 2021: The Square Root Spiral of Theodorus. Link.

Related

Published by thatsmaths