Whether or not you enjoy solving them, those 9×9 grids with numbers and blank cells cannot have escaped your notice. Sudoku puzzles have swept the world since exploding on the scene in 2005. They are found in newspapers everywhere, providing daily amusement to all who like a minor mathematical challenge.
The objective of Sudoku is to complete the grid, starting from a few given numbers or clues, whilst ensuring that each row, each column and each 3×3 block contains all the digits from 1 to 9 once and only once. Sudoku is a combinatorial problem, like a Latin square, where the numbers in each row and column have equal sums, but with the extra constraint that no digit is repeated within a row, column or block.
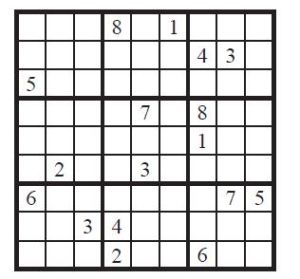
The name Sudoku is a Japanese abbreviation of a phrase meaning “the digits must be single” and the puzzles appeared in Japan around 1984, although they did not originate there, but in New York. There are several variants, but the basic 9×9 grid remains the most popular.
The number of different ways in which a Sudoku grid can be completed has been calculated to be about 6.67×10²¹ (about 7 followed by 21 zeros or 7 sextillion). However, this includes many solutions that are effectively the same, for example where each 1 is changed to a 2, and each 2 to a 1. When symmetries such as this are taken into account, the number of essentially different solutions is 5,472,730,538 or about five and a half billion.
Sudoku puzzles have appeared in The Irish Times for about six years. Another Irish daily paper also publishes them, with the subscript: There’s no maths involved, simply use reasoning and logic! Perhaps this is a reflection of the tragic position of mathematics in our society: it seems that even the idea that something might be “tainted by mathematics” is enough to scare off potential solvers. Could you imagine the promotion of an exhibition in the National Gallery with the slogan: No art involved, just painting and sculpture!
Of course, the solution of Sudoku puzzles is an essentially mathematical activity, involving the application of logical rules and pattern recognition. Construction of puzzles is harder, and analysis of their properties more challenging still, involving the mathematics of combinatorics, permutation group theory, graph colouring and more.
What is the minimum number of clues required to ensure a unique solution? A large number of 17-clue puzzles are known. Until recently, a search for one with 16 clues was under way. However, it has now been shown by Prof Gary McGuire of UCD that this search is futile: there is no 16-clue Sudoku. McGuire and his team used a powerful computer system to search through all possible grids, using a method called a hitting-set algorithm (see report in the Irish Times ). The hitting-set idea has also been used for gene-sequencing analysis and cellular networks.
