Mowing the Lawn in Spirals

Like a circle in a spiral / Like a wheel within a wheel / Never ending or beginning / On an ever-spinning reel.    The Windmills Of Your Mind

Broadly speaking, a spiral curve originates at a central point and gets further away (or closer) as it revolves around the point. Spirals abound in nature, being found at all scales from the whorls at our finger-tips to vast rotating spiral galaxies. The seeds in a sunflower are arranged in spiral segments. In the technical world, the grooves of a gramophone record and the coils of a watch balance-spring are spiral in form.

Spiral Equations

In polar coordinates, the radial distance r ( θ ) from the central point is a monotonic function of the azimuthal angle θ. There are several canonical spiral forms. The simplest is the Archimedean spiral, r = a θ. This is generated by a point moving with uniform speed along a ray that is rotating with constant angular speed. Since the points of intersection with a fixed ray from the origin are evenly spaced with separation 2 π a, it is also called an arithmetic spiral (left panel of figure above). It was described by Archimedes in his work On Spirlas.

More generally, we consider r^k = a^k θ. For k = 2 we get Fermat’s spiral r = a √ θ (centre panel of Fig). For k = –1 we have r = a / θ, which is a hyperbolic spiral (right panel of Fig).

An equiangular spiral is such that every ray from the origin cuts it at the same angle. Its equation is r = a exp ( b θ ). Since b θ = log (r / a ), it is also called a logarithmic spiral and, since the intersection points with a fixed ray form a geometric sequence, the name geometric spiral is also used. Christopher Wren observed that many sea-shells, such at the Nautilus, have logarithmic spiral cross-sections.

Involutes

Suppose you wish to cut the grass. Here is an easy way:

• Erect a stout column in the centre of the lawn;

• Tie the mower to the column with a long rope;

• Start it so that it winds inward in a spiral arc;

• Relax and enjoy the magic of the automower.

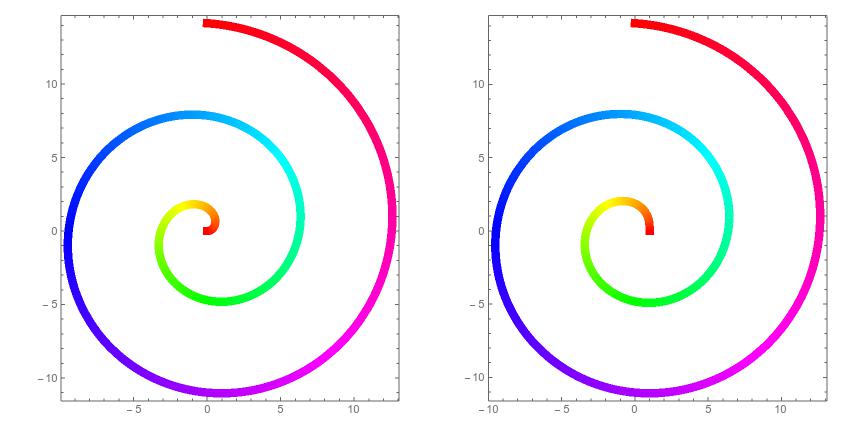
The curve traced by the mower looks like an Archimedean spiral. It is actually slightly different: it is the involute of a circle (namely, the circular cross-section of the central column). The column should be chosen to have circumference 2 π a = D where D is the blade diameter of the mower.

If the column is described by the equations

x = a cos θ ,         y = a sin θ

where a is the radius of the circle, then the curve traced out by the mower is

x = a ( cos θ + θ sin θ ) ,         y = a ( sin θ – θ cos θ )

The radius vector is r² = a² ( 1 + θ ² ) . For θ = 0 we have r = a, whereas, for the Archimedean spiral ( r² = a² θ ² ) we have r = 0 when θ = 0. The two curves are close, but not identical:

Acknowledgement:

This article was inspired by correspondence with Stephen Richardson of Exeter NH.

Sources:

Wells, David, 1991: The Penguin Dictionary of Curious and Interesting Geometry. Penguin Books, ISBN: 9-780-140-11813-1.