Order in the midst of Chaos

We open with a simple mathematical puzzle that is easily solved using only elementary reasoning. Imagine a party where some guests are friends while others are unacquainted. Then the following is always true:

No matter how many guests there are at the party, there are
always two guests with the same number of friends present.

If you wish, try proving this before reading on. The proof is outlined at the end of this post.

Complete-Graphs-6-10 — Complete graphs with 6 to 10 vertices.

Order in the midst of Chaos
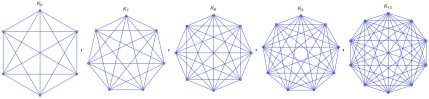
Suppose we have 12 points arranged evenly around a circle. Joining each point or vertex to all the others, we get the complete graph of order 12, or ${\mathbf{K}_{12}}$ . It has ${(12\times 11)/2=66}$ edges. Now suppose we colour each edge red or blue, the choice being completely random. There are ${2^{66} \approx 10^{20}}$ ways to do this. Even allowing for equivalences arising from symmetries, the number of distinct colourings is vast. In general, the arrangement of colours is chaotic.

But is there any order? Can we find three vertices all linked by edges of the same colour? Or four edges? Or five? In graph-theoretic terms, can we find a monochromatic subgraph ${\mathbf{K}_3}$ or ${\mathbf{K}_4}$ or ${\mathbf{K}_5}$ of ${\mathbf{K}_{12}}$ ? Can we find order in the midst of chaos? This is a key aspect of Ramsey Theory.

Ramsey Theory

Frank-Ramsey — Frank P.~Ramsey (1903–1930).

Frank P. Ramsey was a brilliant young British mathematician, born in 1903, who produced some work of stunning originality. He was interested in the logical foundations of mathematics, a topic of great concern during the early twentieth century. In addition to unique mathematical talents, Ramsey was a philosopher and and economist. Despite living only until the age of 26, he made notable contributions to all three of these fields. He was on close friendly terms with philosopher Ludwig Wittgenstein and translated Wittgenstein’s Tractatus Logico-Philosophicus into English.

Ramsey investigated the border-line between order and chaos, and found that, in many systems that appear completely random, order is to be found. In 1930, the year of his death, he published a paper with profound consequences. This work, which overlaps graph theory and combinatorics, has led to an entire branch of mathematics, Ramsey Theory, still a field of active research.

Guests at Parties

In his research on the foundations of mathematics, Ramsey was led to investigate a problem in combinatorics. He considered a simple dinner-party problem: how many guests must there be to ensure that there are either three mutual friends or three mutual strangers? While this seems like a trivial puzzle, it led to breakthroughs that are important in many areas of mathematics. It is especially important in computer science and network analysis.

We can formulate the question in terms of graph theory. We represent the guests by points in a diagram. We join two points by a red edge if the two guests are friends. We join them by a blue edge if they are strangers. The problem may now be stated in geometric terms: what is the minimum number of points, all linked by either a red or a blue edge, such that there must be a red triangle or a blue triangle.

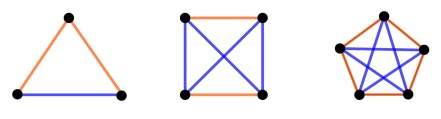
Ramsey-Theory-1 — Parties with 3, 4 or 5 guests may fail to have three mutual friends or three mutual strangers. None of these graphs has a monochromatic triangle.

We can easily show that three guests are not enough: one guest may be friends with the other two, who are unacquainted. Four guests are also insufficient: two pairs of friends who are strangers to the other two result in a graph without any monochromatic triangles. What about five guests. Again, there may be no triangles. An example is shown in the figure above: a blue pentagram within a red pentagon. Ramsey proved that, with six guests, there is always a trio of friends or a trio of strangers; the graph of a six-guest party always has a red or blue triangle.

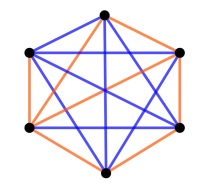
Ramsey-Theory-2 — A party with 6 guests always has three mutual friends or three mutual strangers.

This does not seem to be a significant result. But it is easily generalised. Suppose we require that there be either four mutual friends or four mutual strangers. How many guests would guarantee this? For more points, it is impossible to check by hand. Suppose there are twelve guests. As we saw, with twelve points each joined to the others, ( ${\mathbf{K}_{12}}$ ), the number of possibilities is astronomical. But Frank Ramsey proved that every such dinner-party question has a definite answer. There is always some size that guarantees the presence of a specified sub-structure.

For example, the party size to ensure six mutual friends or strangers has been shown to be somewhere between 102 and 165, but the precise threshold is still unknown. Ramsey also proved far-reaching results in the case where there are an unlimited number of guests. That is, he proved some strong results for infinite graphs. Thus, for random infinite graphs, we can always find highly-ordered structures within them.

Proof of the Party Puzzle

Suppose that there are ${N}$ guests. Then, for each guest, the number of friends has to be one of the elements of the set ${\{0, 1, 2, \dots , N-1\}}$ . That is, there are precisely ${N}$ possibilities. Suppose all guests have a different number of friends. Then someone must have ${N-1}$ friends. But this guest is friends with everyone else. So there is no guest with zero friends; there are only ${N-1}$ possibilities. With ${N}$ guests, this means that (at least) two guests must have the same number of friends [the key idea here is the Pigeonhole Principle].