The Sizes of Sets

The sizes of collections of objects may be determined with the help of one or other of two principles. Let us denote the size of a set ${A}$ by ${\mathfrak{Size}(A)}$ . Then

AP: Aristotle’s Principle. If ${A}$ is a proper subset of ${B}$ , then ${\mathfrak{Size}(A) < \mathfrak{Size}(B)}$ .
CP: Cantor’s Principle. ${\mathfrak{Size}(A) = \mathfrak{Size}(B)}$ if and only if there is a one-to-one correspondence between ${A}$ and ${B}$ .

All is well when we consider only finite sets ${A}$ and ${B}$ . However, when the sets are infinite, these two principles are incompatible. It is not possible to reconcile them, and one or other must be changed or abandoned if a satisfactory theory for measuring infinities is to emerge.

Cantor used a weakened form of Aristotle’s Principle from ${[A\subset B] \implies [\mathfrak{Size}(A) < \mathfrak{Size}(B)]}$ to ${[A\subseteq B] \implies [\mathfrak{Size}(A) \le \mathfrak{Size}(B)]}$ . Thus, it may happen that a proper subset ${A}$ of ${B}$ may be in one-to-one correspondence with ${B}$ .

While this last idea conflicts with intuition, it enabled Cantor to develop a wonderful theory of the cardinality of sets, that has played a powerful role in mathematics ever since.

Galileo’s Paradox

A famous example of a one-to-one correspondence between a set of numbers and one of its proper subsets was discovered and discussed by Galileo. An intriguing paradox appeared in his work, Dialogues Concerning Two New Sciences, in which Galileo presents two opposing arguments:

There are more natural numbers than squares.
The set of natural numbers has as many elements as the set of squares.

In the Dialogues, Salviati observes “that the totality of all numbers is infinite, that the number of squares is infinite, and that the number of their roots is infinite; neither is the number of squares less than the totality of all the numbers, nor the latter greater than the former.”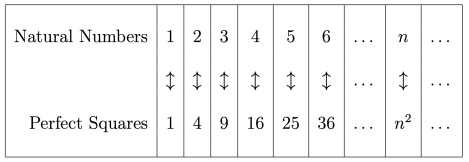

The paradox is illustrated in the Table above, which shows a one-to-one map between numbers and their squares. Salviati deduces that the attributes “equal”, “greater” and “less” are not applicable to infinite sets, but only to finite ones.

Essentially, this means that Galileo himself concluded that size comparison between infinite sets was without meaning. He might have reached a different conclusion if he had persisted in tackling this question, but it appears that he never returned to it.

How Many Even Numbers Are There?

To get a more explicit feel for what is going on, let us start with ${\mathbb{N}}$ , the set of natural numbers. There are several ways of producing from this the set of even numbers. We consider two approaches:

Remove from ${\mathbb{N}}$ all the odd numbers. What is left is the set of even numbers, ${\mathbb{E}}$ . All even numbers are also natural numbers, whereas there are natural numbers (the odd ones) that are not even. We must conclude that ${\mathbb{E}}$ , a proper subset of ${\mathbb{N}}$ , must be smaller than ${\mathbb{N}}$ .
Multiply each number in ${\mathbb{N}}$ by ${2}$ . From each natural number ${n}$ we obtain the even number ${2n}$ . All the natural numbers are used and all the even numbers are produced. There is a one-to-one correspondence between ${\mathbb{N}}$ and ${\mathbb{E}}$ . Clearly, we must conclude that the two sets are “the same size”.

Cantor’s method of measuring the sizes of sets has been dominant for over a century. However, recently, alternative methods have been proposed. For one such approach, called numerosities, see Benci and Di Nasso (2003). In this case, Aristotle’s Principle is maintained, while Cantor’s Principle, “ ${\mathfrak{Size}(A) = \mathfrak{Size}(B)}$ if and only if there is a one-to-one correspondence between ${A}$ and ${B}$ ” is weakened to “If ${\mathfrak{Size}(A) = \mathfrak{Size}(B)}$ , then there is a one-to-one correspondence between ${A}$ and ${B}$ .” Thus, two sets that are in a one-to-one correspondence may have different numerosities.

I hope to write about these developments in a later post.

Sources

${\bullet}$ Galileo (1939). Dialogues Concerning Two New Sciences. Evanston, IL: Northwestern University. Reprinted by Dover 1954.

${\bullet}$ Benci, Vieri and Mauro Di Nasso, 2003: Numerosities of labelled sets: a new way of counting. Advances in Maths., 173, 50–67.

Related

Published by thatsmaths