Puzzle: However fast a train is travelling, part of it is moving backwards. Which part?
For the answer, see the end of this post.
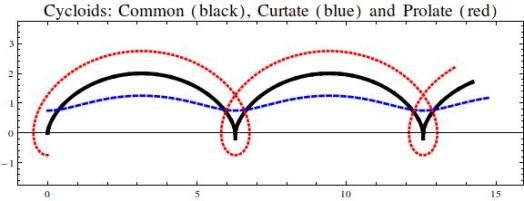
Imagine a small light fixed to the rim of a bicycle wheel. As the bike moves, the light rises and falls in a series of arches. A long-exposure nocturnal photograph would show a cycloid, the curve traced out by a point on a circle as it rolls along a straight line. A light at the wheel-hub traces out a straight line. If the light is at the mid-point of a spoke, the curve it follows is a curtate cycloid. A point outside the rim traces out a prolate cycloid, with a backward loop. [TM076; or search for “thatsmaths” at irishtimes.com ]
Cycloids were studied by many leading mathematicians over the past five-hundred years. The name cycloid originates with Galileo, who studied the curve in detail. The story of Galileo dropping objects from the Leaning Tower of Pisa is well-known. Although he could not have known it, a falling object traces out an arc of an inverted cycloid. This is due to the tiny deflection caused by the Earth’s rotation. Moreover, an object thrown straight upward follows the loop of a prolate cycloid, landing slightly to the west of its launch-point.
Pascal’s Toothache
Blaise Pascal, who had abandoned mathematics for theology, found relief from a toothache by contemplating the properties of cycloids. Taking this to be a sign from above, he resumed his mathematical researches. Pascal proposed some problems on the cycloid and one of the respondents was Christopher Wren, better known as the architect of St. Paul’s Cathedral in London. Wren proved that the length of a cycloid arch is four times the diameter of the circle that generates it. Today, this is an easy problem in integral calculus but in 1658 it was a formidable achievement.
The bob of a pendulum traces out a circular arc as it swings. The period, or time for a full to-and-fro oscillation, depends on the arc-length or swing amplitude, increasing slightly for a wider arc. This complicates the measurement of time with a pendulum clock. If the circular arc is replaced by a cycloidal arc, the period remains constant regardless of amplitude. For this reason the cycloid is said to be isochronous. The Dutch scientist Christiaan Huygens discovered this, and built a chronometer using an ingenious method of achieving a cycloidal swing.
The Lion’s Claw
In 1696, Johann Bernoulli posed a problem that he called the brachistochrone – or shortest time – problem: find the path along which gravity brings a mass from one point to another one not directly below it. The five mathematicians who responded included Newton, Leibniz and Johann’s brother Jakob. The desired path is a cycloid.
The story goes that Newton received the problem one evening, upon returning from the Royal Mint, where he was Master. He stayed up late working on it and by 4 a.m. he had obtained a solution, which he mailed later that morning. Although his solution was anonymous, Bernoulli immediately perceived its authority and brilliance, giving his reaction in the classic phrase “ex ungue leonem”, the lion is recognized from his claw.
Cycloid arches have been used in some modern buildings, a notable example being the Kimbell Art Museum in Fort Worth, Texas, designed by the renowned architect Louis I. Kahn. Like many classical buildings, the museum is based on a consistent mathematical model. The basic plan is composed of cycloid vaults arranged in parallel units. These vaults have gently rising sides, giving the impression of monumentality. This geometric form is capable of supporting its own weight and can withstand heavy pressure.
In the atmosphere, the rotation of the Earth generates cycloidal motion: ice-bergs and floating buoys have been seen to trace multiple loops of a prolate cycloid. Finally, epicycloids and hypocycloids are used in modern gear systems as they provide good contact between meshed gear teeth giving efficient energy transmission.
Equation for the Cycloid
The motion of a point on a unit circle rolling on a horizontal line ( y = 0 ) is made up of two parts: linear motion of the centre and circular motion of the point relative to the centre. Assuming that the point is at the origin at time t =0 and moves with unit speed, the coordinates of the centre are x = t, y = 1. For pure rolling with unit angular velocity 
x = t – sin t y = 1 – cos t
We can solve the second equation for t, getting t = arccos(1 – y). Substituting this into the first equation we get
x = arccos(1 – y) – sin[arccos(1 – y)] = arccos(1 – y) – \sqrt y(2-y)
It is a simple matter to write the equations for the curtate and prolate cycloids, by adjusting the amplitude of the circular component. The three cases are included in the equations
x = t – a sin t y = 1 – a cos t
where a <1 for the curtate cycloid and a >1 for the prolate cycloid.
The area under an arch of a cycloid is 3π, and the length of a single arch is 8.
Answer to puzzle
A point on the wheel-flange of a railway locomotive is outside the rolling surface of the wheel and, when below it, moves backwards in the loop of a prolate cycloid. The faster the train goes, the faster the reverse motion!
ThatsMaths 