The numerous connections between mathematics and music have long intrigued practitioners of both. For centuries scholars and musicians have used maths to analyze music and also to create it. Many of the great composers had a deep understanding of the mathematical principles underlying music. Johann Sebastian Bach was the grand master of structural innovation and invention in music. While his compositions are the free creations of a genius, they have a fundamentally mathematical basis [See TM116 or search for “thatsmaths” at irishtimes.com].

Musical sounds may be broken down into pure waves, each with a fixed frequency or number of vibrations per second. The Pythagoreans noticed that there was a connection between numerical ratios and consonant sounds. Galileo explained consonance in terms of periodic waveforms that do not “keep the ear in perpetual torment”. More sophisticated theorizing today depends on psychoacoustics.
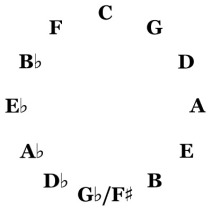
Waves with small integer frequency ratios harmonize, with sonorous effect. The entire chromatic scale can be made up of octaves and fifths, or ratios of 2:1 and 3:2. Starting from a base note, we generate new harmonics by repeatedly rescaling by 3/2 and, as necessary, halving to remain within an octave. This gives us the “Circle of Fifths”.
Mathematicians emphasize the aesthetic aspect of their work. Both mathematics and music are dominated by patterns. The mathematician’s patterns, like those of the composer, must be beautiful; the ideas must fit together in a harmonious way. As G H Hardy put it, “Beauty is the first test: there is no permanent place in the world for ugly mathematics”.
Symmetry
Symmetry is an essential aspect of all music, so it is not surprising that group theory, the mathematical framework for symmetry, has been applied to musical analysis. The musical techniques of transposition, inversion and retrogression can all be interpreted as group operations, and this perspective has shed new light on old compositions. Many composers have used geometric transformations as a compositional device. Transformations and symmetries provide a range of tools for composers to enrich their creations. Thus, a chosen theme may be transposed, inverted or reflected in time to produce variations.
Probability has also been used in musical composition. One minuet, attributed to Haydn, has six parallel staves, the one to be played being chosen by a dice-roll. Each dice throw is independent of the previous one. With sixteen bars in total, there are about 2.7 trillion possible variations.

Any graph or signal can be interpreted in musical terms by superimposing it on a stave to define a melody (though not necessarily a pleasant one). Melodies have a geometric shape: by “joining the dots” in a musical score we generate a graph giving the “shape” of the composition (see figure above). The Parsons code is a simple notation used to identify a piece of music through up and down changes of pitch. We can search for any piece of music by inputting the Parsons code at the Musipedia website, http://www.musipedia.org/.
The interface between maths and music is rich and complex. The nineteenth century English mathematician J J Sylvester put it thus: “May not music be described as the mathematics of sense, mathematics as the music of reason, the soul of each the same?”. We have mentioned just a few of the connections. Mathematics provides a framework for appreciating music, but music has a profound emotional content that no currently available variety of mathematics can explain.
