In the last post, we saw how Yves Meyer won the Abel Prize for his work with wavelets. Wavelets make it easy to analyse, compress and transmit information of all sorts, to eliminate noise and to perform numerical calculations. Let us take a look at how they came to be invented.
Fourier’s Marvellous Idea.
In the early 1900s, Joseph Fourier showed how to analyse general functions into simple sinusoidal components and this enabled scientists to solve a range of important problems. However, Fourier’s method has drawbacks as well as advantages. Since a sine wave extends over an infinite time, local properties of the signal become global features of the transform. For example, a narrow spike in the input becomes a superposition of a large number of frequencies.
Many interesting signals are restricted in time. For example, a musical composition is made up by combining short sounds of different frequencies. In the Fourier transform of a musical composition, the sinusoidal components, which extend over the full dimension of time, must cancel exactly throughout the entire infinite period before the music starts and the eternity after it ends. This makes us question whether such sinusoidal functions are really suitable: can we find functions that are more in sympathy with the time-bounded nature of the musical composition?
The Emergence of Wavelets
The need for more local basis functions was a driving force for the development of wavelets. Scientists invented a range of techniques that replaced the infinite sin functions by functions confined in time. Short-time Fourier analysis or windowed Fourier analysis was one such method. But a comprehensive mathematical theory was lacking. Wavelet analysis provided a rigorous framework for all these ad hoc methods.
Wavelets are oscillations that are confined in time or scale. We can think of a sine wave multiplied by a Gaussian bell function that tends rapidly to zero as we move away from the peak.

This is the “mother wavelet” and a whole family of wavelets can be obtained by dilating it (stretching or compressing it). We also translate the wavelets in time to analyse different segments of the signal. Thus, we can zoom in on interesting features such as discontinuities or sharp spikes, and analyse them without the complication of what may be happening at other times.
Wavelets automatically adapt to the different features of a signal, using a small window or width to look at short time high frequency aspects and a large window for long-lived low frequency components. This technique is what is called multi-resolution. As Yves Mayer puts it: “You play with the width of the wavelet to catch the rhythm of the signal”.
Since wavelets adapt to the nature of the signal, great compression is possible: only those wavelets with significant amplitude need to be retained. Often, an input signal with 100,000 values can be reduced to 10,000 wavelet coefficients. Those components with negligible values are simply dropped.
Continuous Wavelet Transform
The continuous wavelet transform of a function f(t) is given by an integral

The function ψ is used to generate a family of wavelets ψ(at+b) where a compresses or stretches the function and b translates it in time. This transform is strongly redundant: we have replaced a function of a single variable, f(t), by a function of two variables, c(a,b).
Researchers soon found a way of generating sets of wavelets that are orthogonal: the integral of any member multiplied by another vanishes. This enabled perfect reconstruction of the signal while eliminating redundancy. This led straight to economical wavelet transforms: the transform contains the same number of points as the input signal.

Computation with wavelets is very efficient. There is a Fast Wavelet Transform (FWT) analogous to the FFT of Fourier analysis. Computations with the FWT scale linearly; that is, if the problem size is doubled, so is the amount of computation. This means that many problems that were utterly intractable before wavelets can now be solved quite easily. It makes computations feasible that would otherwise be impossible!
With Fourier analysis, there is very little lee-way. Scientists simply plug the input signal into a software package and generate the Fourier transform. With wavelets, the range of choices is much wider, and a judicious selection is necessary: experience is vital to choose the best wavelet formulation.
Wavelets are an extension of Fourier analysis. The two techniques are complementary: Fourier analysis is suitable for regular periodic signals while wavelets can handle non-stationary signals with spikes and discontinuities.
Data Compression
Wavelets have been used to analyse a wide range of data, such as photographs, medical images, video compression, seismic waves and electrocardiograms. Many images have a high level of redundancy. Take a photograph of a tree against a background of a clear blue sky. The details of the leaves and trunk may vary on small scales but have no large-scale features. The sky may be uniform, requiring just a few large-scale wavelet components. A high level of compression is usually possible, reducing storage and transmission times by an order of magnitude or more. A cardiogram may have sharp isolated features, but its structure has much regularity and a small number of wavelet components can faithfully represent it.
Fingerprints: automatic identification systems.
Wavelets have been used for the archival and automatic identification of fingerprints. The image below shows the original print (left) and an image compressed by a factor of 26 (image credit: Chris Brislawn, Los Alamos National Laboratory). To the naked eye the two images are indistinguishable.

The figure below shows a signal with frequency decreasing and then increasing again. The continuous wavelet transform is also shown, with time on the horizontal axis and frequency on the vertical axis. It makes clear that the frequencies of the principle wavelet components decrease and then increase. The diagram is reminiscent of a musical score, with time on the horizontal axis and pitch or frequency on the vertical.

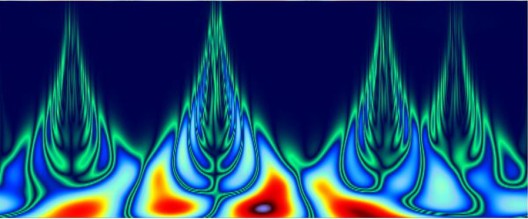
In the final figure, a signal with several high-frequency (HF) bursts is shown. The wavelet transform, in time-frequency space, resembles flaming fingers pointing towards the times when the frequency of the signal is maximum. The HF episodes are clearly indicated. Behaviour of this sort is found in fluid flow with intermittent turbulence: there are quiet periods, interrupted by bursts of violent, turbulent motion.

Sources
Barbara Burke Hubbard, 1996: The World According to Wavelets. A K Peters, Ltd. xx+264pp. ISBN: 9-781-56881-047-4. [The author interviewed many of the originators of the theory of wavelets, including Yves Mayer, winner of the 2017 Abel Prize].
