The Parthenon is a masterpiece of symmetry and proportion. This temple to the Goddess Athena was built with pure white marble quarried at Pentelikon, about 20km from Athens. It was erected without mortar or cement, the stones being carved to great accuracy and locked together by iron clamps. The building and sculptures were completed in just 15 years, between 447 and 432 BC. [TM141 or search for “thatsmaths” at irishtimes.com].
The Parthenon shows how brilliantly the Greeks had mastered geometric principles. They saw mathematics as a means to understand the Divine. They achieved global perfection through deliberate departure from local precision. Minor geometric irregularities were incorporated by the architects, Iktinos and Kallikrates, to enhance the beauty of the building. It is paradoxical that these modifications create the impression of great geometric perfection, even though they involve deliberate departures from strict regularity.
Phidias, Master Sculptor
Within the treasury of the Parthenon stood an 11 metre statue of Athena, carved in ivory with armour of pure gold. Sadly, nothing remains of this statue. It was one of the greatest creations of Phidias, the undisputed genius of Greek sculpture, who oversaw all the sculptural work. The most excellent carving is found in the frieze panels, many of which are now in the British Museum.
The ratio of the longer side of the Parthenon to the shorter side is root-five to one. The square root of 5 is the number that, multiplied by itself, yields 5. Its value is about 2.236. The Greeks were captivated by this number, which is an irrational number, not equal to the ratio of two whole numbers. It is easily constructed, bieng the diagonal length for a rectangle with sides 1 and 2. It has been argued that the façade of the Parthenon has proportions of the golden ratio, widely held to be the most aesthetically pleasing shape. The golden number is equal to (1+√5)/2, or approximately 1.618.
Optical refinements
Despite appearances, there are few perfectly straight lines or right angles in the Parthenon. The observer sees the eight columns of the façade as a perfectly regular array, but this is achieved by deliberately introducing subtle distortions called “optical refinements”. To avoid an apparent sagging effect, the base of the façade is about 6 cm higher at its centre than at the corners. This curvature can be clearly seen by viewing it from close to a corner.
The shape of the column shafts, and their slight tilt from the vertical, are said to correct optical distortions so that the building appears to be perfectly regular. The columns taper towards the top, but also swell slightly part of the way up, to avoid an impression of narrowing at the centre. The corner columns are marginally wider, to counteract another visual effect; without this adjustment, they would appear thinner than the inner columns.
The columns are not exactly equidistant, the outer ones being slightly closer together. Neither are the columns precisely vertical; they slope imperceptibly inwards. It has been estimated that the end columns, if continued upwards, would meet several kilometres above the Parthenon. These refinements required a remarkable degree of precision, and deep understanding of both geometry and the subtleties of human visual perception.
The Acropolis
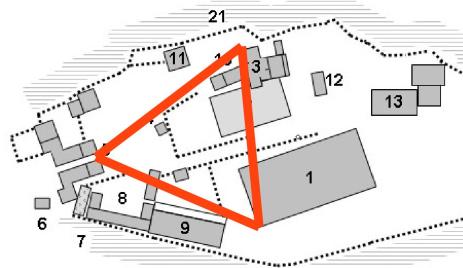
At first glance, the positioning of the buildings on the Acropolis appears to be haphazard, without any clear plan. However, researchers have noted a systematic arrangement of the three primary buildings, the monumental gateway building or Propylaea, the Parthenon and the Erechtheion. The layout of the buildings is based on a system of rays emanating from a vantage-point at the Propylaea, giving an optimum view of the façade of the Parthenon. From this vantage-point, the outermost limits of the other two buildings form an angle of 60 degrees, and the three points form an equilateral triangle (see figure), a geometric form associated with Athena.
Some scholars dispute the significance of the irregularities in the Parthenon, ascribing them to inevitable deviations from perfection in its construction, or to more prosaic purposes. For example, the curvature of the base may have been introduced to facilitate drainage, rather than for aesthetic reasons. Whatever the truth, it is indisputable that the Parthenon is an amazing celebration of the power of geometry, an anthem to the breadth and beauty of mathematics.
Sources
Video: The Acropolis of Athens in ancient Greece – Dimensions and proportions of Parthenon. https://www.youtube.com/watch?v=XN44e3jmDSA
ThatsMaths 