The links between music and mathematics stretch back to Pythagoras and many leading mathematicians have studied the theory of music. Music and mathematics were pillars of the Quadrivium, the four-fold way that formed the basis of higher education for thousands of years. Music was a central theme for Johannes Kepler in his Harmonices Mundi – Harmony of the World, and René Descartes’ first work was a compendium of music.
Leonhard Euler retained an interest in music throughout his long life. His early notebooks contain work on theoretical systems of music. He considered music and mathematics as part of a single coordinated system, and his study of music inspired his work on number theory, fluid mechanics and even topology. His book Tentamen novae theorae musicae, published in 1739, was completed in 1730 when Euler was just 23 years old. This work did not attract great interest at the time and indeed was described as “too mathematical for musicians and too musical for mathematicians.”
In the Tentamen, Euler developed an index to indicate the characteristics of different combinations of notes. It was a quantitative measure of the pleasantness of musical intervals and chords. He called it his Gradus Suavitatis, or Degree of Agreeableness.
Gradus Suavitatis (GV) or Degree of Agreeableness
Pythagoras had shown that chords formed by notes having simple whole-number relationships were pleasant or harmonious, and that combinations of notes lacking this connection tended to clash or be dissonant. Euler wanted to advance beyond this. He graded different intervals by means of a number that he called the gradus suavitatis; this may be translated as the degree of agreeableness, sweetness or tunefulness. He was familiar with the concept of the well-tempered scale, in which the ratios between notes are irrational numbers. However, he argued that the human ear is not bothered by these irrational proportions, since irrational numbers can be approximated by whole-number ratios.
Euler assigned a degree d = 1 to unisons (effectively the same note sounded twice), and a degree of 2 to an octave. For ratios 1 : p, where p is a prime number, he set the degree to be d = p. Thus, an octave plus a fifth (say, from C4 to G5) would have degree d = 3 since its ratio is 1 : 3. He arrived at an expression for the ratio for any composite number m with n prime factors summing to s; the degree of the interval with ratio 1 : m was given by
d = s – n + 1
He also concluded that the ratio p : q had the same degree as 1 : p q and, for a triad, p : q : r had the same degree as 1 : p q r. Here he let m be the least common multiple of the components p and q or p, q and r. Then s was the sum of the prime factors of m and n was the number of factors.
For example, the pure fifth has a frequency ratio 3 : 2, with the same degree as 1 : 2 x 3 or d = 4. And for the major triad, with proportions 4 : 5 : 6, the least common multiple is 60 = 2 x 2 x 3 x 5, so that m = 60, s = 12 and n = 4, leading to the degree d = 12 – 4 + 1 = 9.
GV for Just Intonation
The table below shows the ratios for the octave tuned in just intonation. This is a refinement of Pythagorean tuning to reduce the sizes of the whole-number ratios. Using the above formula, it is a simple matter to calulate the gradus suavitatis, and the values are added in the bottom row of the table.
Euler tabulated the values of his GV degree for a range of interval ratios, including many ratios that rarely if ever occur in classical music. His table is reproduced below, with the seven intervals of the just-intonation scale marked by red ellipses (the unison, 1 : 1 with d = 1 is omitted).
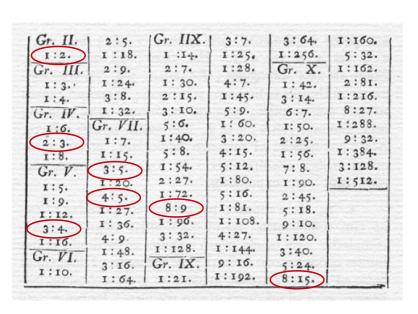
The major triad C–E–G with ratio 4 : 5 : 6 has degree d = 9. In contrast, a minor triad such as E–G–B has approximate ratio 5 : 6 : 7 and degree d = 14. This is one way to account for its quality of “sadness”, compared to the relative joy of the major chord.
Euler’s scheme has been reviewed by Pesic (2013), who notes some curious aspects of his GV measure. Euler assigns the same degree to the interval 1 : p q r and to the triad p : q : r, which is contrary to expectations. More surprisingly, his scheme gives the same value, d = 9, to the major triad C–E–G and to the dissonant major seventh chord C–E–G–B.
Pesic draws an analogy between Euler’s GV formula d = s – n + 1 and his famous polyhedron formula V – E + F = 2. The former categorizes musical intervals, while the latter, at least in its more general form χ = V – E + F, categorizes surfaces of equal topological genus.
Sources:
Euler, Leonhard, 1839: Tentamen Theorae Novae Musicae. S. Petersburg Acad Sci.
Peter Pesic, 2013: Euler’s Musical Mathematics. Mathematical Intelligencer, 35, 2, 35-43. DOI 10.1007/s00283-013-9369-5
ThatsMaths 