Listing the Rational Numbers III: The Calkin-Wilf Tree

Calkin-Wilf-Tree The rational numbers are countable: they can be put into one-to-one correspondence with the natural numbers. In previous articles we showed how the rationals can be presented as a list that includes each rational precisely once. One approach leads to the Farey Sequences. A second, related, approach gives us the Stern-Brocot Tree. Here, we introduce another tree structure, The Calkin-Wilf Tree.

The Calkin-Wilf Tree

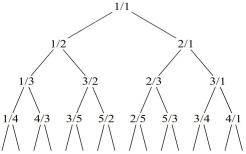
The Calkin-Wilf Tree is quite similar to the Stern-Brocot tree, but the differences are interesting. The structure, devised by Neil Calkin and Herbert Wilf in 2000, contains each positive rational number precisely once. The tree starts with the root value ${{1}/{1}}$ .

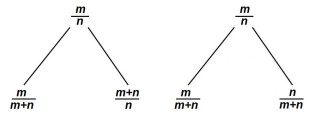
Each rational in the tree has two “children”. For the entry ${m/n}$ , the children are ${m/(m+n)}$ and ${(m+n)/n}$ . We note that the “left child” ${m/(m+n)}$ is always smaller than 1 while the “right child” ${(m+n)/n}$ is always greater than 1.

At Level 1 we have one number, ${\{\frac{1}{1}\}}$ , and at Level 2 we have two, ${\{\frac{1}{2},\frac{2}{1}\}}$ . At Level ${k}$ there are ${2^k}$ ratios. To construct Level ${k+1}$ , we form thetwo children of each entry in Level ${k}$ . Every branch of the tree bifurcates at every level.

The Calkin-Wilf tree [Image: Wikimedia Commons].

The CW Tree is complete

The Calkin-Wilf tree is complete: it is easy to show that each positive rational number occurs precisely once. Considering a rational number ${c/d}$ less than 1, we see that it is the child of ${c/(d-c)}$ which has a smaller denominator. For a rational number ${e/f}$ greater than 1, the parent is ${(e-f)/f}$ which has a smaller numerator. If there are any missing rationals, there must be one ${m/n}$ such that ${m+n}$ is minimum. But we can link ${m/n}$ back to either ${m/(n-m)}$ or to ${(m-n)/n}$ . Both of these numbers have a sum of numerator and denominator that is less than ${m+n}$ . This contradiction forces us to conclude that no such ${m/n}$ exists and that the tree must include all positive rationals.

The Kepler Tree

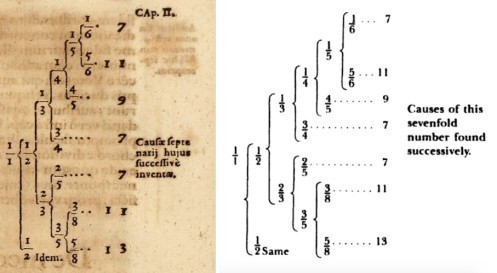
There is nothing new under the Sun: in his book Harmonices Mundi (The Harmony of the World, 1619), Johannes Kepler presented a tree structure that is closely related to the Calkin-Wilf tree. Kepler’s tree is shown in the FIgure below (from Kepler, Book 3, page 27). It contains all rational numbers between ${0}$ and ${1}$ . Chapter 2 of Book 3 is entitled “On the Harmonic Divisions of the String”. Kepler analyses the properties of a string divided into two parts having small number ratios. On page 163 of Harmonices Mundi he writes: “The harmonic divisions of a single string are seven in number, not more.” He presents a numerical tree giving the origin of the seven ratios. The root of the tree is ${1/2}$ and, for any entry ${m/n}$ the two children are ${m/(m+n)}$ and ${n/(m+n)}$ .

The tree in Kepler’s Harmonices Mundi, Book III, pg. 27 (left) and the corresponding figure from the translation, The Harmony of the World (right).

Kepler writes “Let the diligent reader read what I wrote about these divisions 22 years ago in The Secret of the Universe, Chapter XII.” He then explains at length how he came to realize that the origin of the seven harmonies is to be found in the properties of constructable plane polygons. He stressed that he followed the evidence of his own ears in reaching his conclusions, not just blind reasoning, which could “drag the ears astray, ordering them to become deaf”.

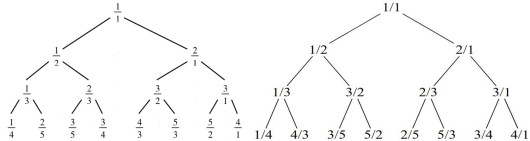
The elements of the Calkin-Wilf tree and Kepler’s tree are shown below. Notice that, while the CW tree includes all positive rationals, the entries in Kepler’s tree are confined to the interval ${(0,1)}$ .

Construction of the Calkin-Wilf tree (left)
and Kepler’s tree (right).

Stern-Brocot and Calkin-Wilf Trees

The construction of the Calkin-Wilf Tree is simpler than that of the Stern-Brocot tree: There is no need to introduce boundary values ${0/1}$ and ${1/0}$ , and only one value is used to generate two new values. Everything springs from the root ${1/1}$ . But CW lacks some nice properties of the SB tree: in the latter, the values at each level are arranged in increasing magnitude, and the structure can be used as a binary search tree. Both CW and SB are binary trees and both contain all positive rational numbers. Moreover, the same numbers appear at each level in each.

The Stern-Brocot tree (left) and Calkin-Wilf tree (right).

Sources

${\bullet}$ Calkin, Neil Calkin and Herbert S. Wilf, 1999: Recounting the rationals. American Mathematical Monthly, 107, (4), 360–363. PDF

${\bullet}$ Johannes Kepler: 1619: Harmonices Mundi. Translation (The Harmony of the World) by Eric J Aiton et al. Series: Memoirs of the American Philosophical Society, 209. American Philosophical Society, Philadelphia, 1997.

${\bullet}$ Wikipedia article Calkin-Wilf Tree.

ThatsMaths