Archimedes and the Volume of a Sphere

One of the most remarkable and important mathematical results obtained by Archimedes was the determination of the volume of a sphere. Archimedes used a technique of sub-dividing the volume into slices of known cross-sectional area and adding up, or integrating, the volumes of the slices. This was essentially an application of a technique that was — close to two thousand years later — formulated as integral calculus.

SphConCyl-5 — Cone, sphere and cylinder on the same base. The volumes are in the ratios 1 : 2 : 3 [image from mathigon.org].

Archimedes considered three volumes: a cylinder, cone and sphere, all on a base having the same area. Thus, the sphere had diameter ${D = 2r}$ , the cylinder had diameter ${D = 2r}$ and height ${H = 2r}$ , and the cone had base diameter ${D = 2r}$ and height ${H = 2r}$ (see Figure).

Archimedes was able to show that if the volumes of the cone and sphere are added, the result is the volume of the cylinder. Moreover, he showed that the three volumes are in the ratio ${1\ :\ 2\ :\ 3}$ . Thus, in particular, the volume of the sphere is two thirds of the volume of the cylinder.

Rearranging the Cone

It is far from obvious from the figure above how the cone and sphere add up to the cylinder. However, if we `rearrange’ the conic volume, things become clearer. We note that a cone with half the height ( ${H/2 = r}$ ) has half the volume. So, we replace the cone by a double cone, each half of height ${r}$ , with centre-point at the centre of the sphere (see Figure below). Now it is clear that in a horizontal slice, the cross-section of the sphere is greatest at the equator and least at the poles. Contrariwise, the cross-section of the cone is greatest near the top and bottom, and least near the centre-point. Thus, it is not unreasonable to speculate that the sum of the two cross-section areas might be equal.

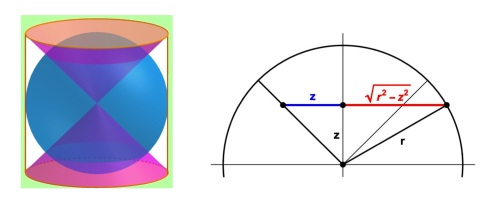
SphConCyl-22 — (a) Sphere, cone and cylinder on the same base. (b) Cross-section of sphere and cone. Radius of horizontal slice at height ${z}$ is ${z}$ for the cone and ${\sqrt{r^2-z^2}}$ for the sphere.

(a) Sphere, cone and cylinder on the same base. (b) Cross-section of sphere and cone. Radius of horizontal slice at height ${z}$ is ${z}$ for the cone and ${\sqrt{r^2-z^2}}$ for the sphere.

We let ${z}$ denote the vertical coordinate measured from the centre of the sphere, and ${\Delta z}$ be a small increment of height. Then the volumes of thin slices of the cone and sphere at height ${z}$ are

$\displaystyle \Delta V_{\rm CON} = \pi z^2 \Delta z \qquad \quad \Delta V_{\rm SPH} = \pi (\sqrt{r^2 - z^2})^2 \Delta z = \pi(r^2-z^2) \Delta z \,.$

Adding these, we get the volume of a thin horizontal slice of the cylinder:

$\displaystyle \Delta V_{\rm CON} + \Delta V_{\rm SPH} = \pi r^2 \Delta z = \Delta V_{\rm CYL} \,.$

This does not vary with height ${z}$ . Finally, adding up the volumes of all the horizontal slices, we find that

$\displaystyle V_{\rm CON} + V_{\rm SPH} = V_{\rm CYL} = \pi r^2 H \,.$

Integral Calculus Foreshadowed

It is not quite so simple to show that

$\displaystyle V_{\rm CON} = \frac{1}{3} V_{\rm CYL} \qquad\mbox{and}\qquad V_{\rm SPH} = \frac{2}{3} V_{\rm CYL} \,.$

However, this was well within the capability of the brilliant Archimedes. Eudoxus had shown earlier that the volume of a pyramid is one-third the volume of a prism with the same base and altitude. Considering pyramids with polygonal bases, he came to the conclusion that the volume of a cone is one-third that of the corresponding cylinder. This result appeared as Proposition 10 of Book XII of Euclid’s Elements.

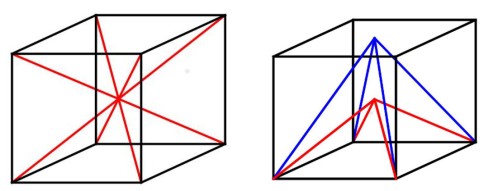
It is quite easy to show that a pyramid of height ${H}$ on a base of area ${A}$ has volume ${V = \frac{1}{3} A H}$ . The factor of one-third can be understood by considering a cube of side ${L}$ (see Figure below). The four lines joining opposite vertices divide the cube into six congruent pyramids, each face of the cube being the base of a pyramid. So, each pyramid must have volume ${\frac{1}{6}L^3}$ . Therefore, a pyramid having the same height as the cube has volume ${\frac{1}{3}L^3}$ (see blue pyramid in Figure below).

Cube-Pyramids-6+1 — Pyramids in a cube. The blue pyramid is one-third the volume of the cube.

Archimedes invented a method that was later re-discovered and became known as Cavalieri’s principle. This involves slicing solids with a family of parallel planes. In particular, if we have two solids and if each plane cuts them both into cross-sections of equal area, then the two solids have equal volumes.

Using this method, Archimedes was able to show that a cone had the same volume as a a pyramid with the same base area and height. Supposing that two solid bodies are bounded between two parallel planes, and every plane parallel to these two planes cuts both solids in cross-sections of equal area, then the two solids have equal volumes.

Archimedes concluded that the cone must have one-third the volume of the cylinder and, since the cone and sphere together equal the cylinder in volume, the sphere must have two-thirds the volume of the cylinder:

$\displaystyle V_{\rm SPH} = \frac{2}{3} V_{\rm CYL} = \frac{4}{3}\pi r^3 \,.$

Archimedes’ method of finding areas and volumes was not surpasses until modern times. The way he discovered these results was not known until a copy of his treatise The Method was discovered in Istanbul in 1906 (see article on the Archimedes Palimpsest).

Archimedes’ Tomb

Archimedes died during the Siege of Syracuse, murdered by a Roman soldier, despite the orders of the commander, General Marcellus, that he should not be harmed. The Roman writer Cicero visited his tomb about a century after Archimedes’ death. He described a carving of a sphere and a cylinder on the head-stone. It is said that Archimedes had requested this memorial to commemorate what he regarded as his greatest mathematical discovery.

Sources

${\bullet}$ Maths is Fun website: Cone, Sphere and Cylinder.

${\bullet}$ That’s Maths article on the Archimedes Palimpsest.

${\bullet}$ Wikipedia article Archimedes.

${\bullet}$ Wikipedia article Cavalieri’s Principle.

Related

Published by thatsmaths