The Axiom of Choice: Shoes & Socks and Non-constructive Proofs

Recall Euclid’s proof that there is no limit to the list of prime numbers. One way to show this is that, by assuming that some number ${p}$ is the largest prime, we arrive at a contradiction. The idea is simple yet powerful.

AoC: each jar is a set, its elements are the marbles [image Wikimedia Commons].

A Non-constructive Proof

Suppose ${p}$ is prime and there are no prime numbers greater than ${p}$ . We form the number

$\displaystyle K = p! + 1 \,.$

It is clear that every number less than or equal to ${p}$ divides ${p!}$ . Therefore each of these numbers leaves a remainder of ${1}$ when divided into ${K}$ , so none of them divides ${K}$ .

Now ${K}$ is either prime or composite. If it is prime, it is a prime number greater than ${p}$ , so ${p}$ cannot be the largest prime. If ${K}$ is not prime, it must have prime factors; but all of them must be greater than ${p}$ so, again, there must exist a prime number greater than ${p}$ .

This line of argument depends on the Law of the Excluded Middle: any well-formed mathematical statement is either true or false. Suppose the statement in question is

“The set of primes is finite”.

Then, the above argument has shown that it cannot be true so, by the Law of the Excluded Middle, it must be false. Few people would argue with this result, but it is not entirely satisfactory, because it is non-constructive: while we have shown that there must be a prime larger than any prime ${p}$ , we have not found it.

And finding it can be difficult. For example, if we take ${p=7}$ then ${K = 5051}$ which turns out to be a perfect square, ${71^2}$ , and ${71}$ is a prime greater than ${7}$ . But taking ${p=11}$ , we get ${K = 39{,}916{,}801}$ . Although this turns out to be prime, it is not trivial to show this. Clearly, for large ${p}$ , it is completely impractical to check the primality of ${p!+1}$ .

We can improve on the proof, reducing the computation, by replacing “factorial ${p}$ ” by “primorial ${p}$ ”. The primorial function p# ( p(hash) ) is defined thus:

$\displaystyle p_n(hash) = \prod_{k=1}^n p_k \,.$

Thus, ${p_7(hash) = (2\times3\times5\times7\times11\times13\times17) = 510{,}510}$ , which is much smaller than ${17! = 355,687,428,096,000}$ . But this does not change the principle of the above argument.

The Axiom of Choice (AoC)

Most people who encounter a non-constructive proof find it acceptable, but wonder if there is a constructive proof that might provide greater insight and be more informative. Sometimes that is the case and sometimes not.

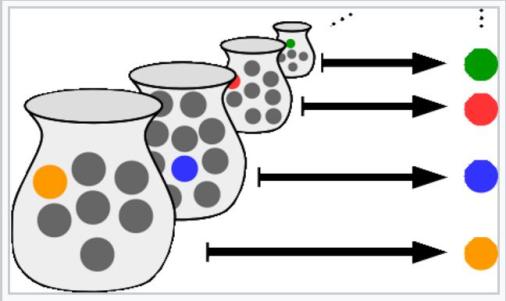
Many mathematical results depend for their proof on an axiom called the Axiom of Choice (AoC). This may be expressed in many equivalent ways. Essentially, it says that, if we have a family of sets ${X_i}$ , where ${i}$ ranges over some index set ${I}$ , we can form a new set comprising a single element ${x_i}$ from each set ${X_i}$ (see Figure above). This seems obvious; and it is obvious for a finite family of sets. But, for an infinite family of sets, we may not be able to provide an explicit specification of how the elements ${x_i}$ are chosen.

A clever metaphor was devised by Bertrand Russell. Consider first an infinite collection of pairs of shoes; we can form a new set by selecting the left shoe from each pair. But suppose now we have an infinite collection of pairs of socks. As the left and right socks are indistinguishable, we have no rule governing how a member of each pair is to be chosen.

In general, where the Axiom of Choice is required for a proof, it is an indication that the proof is non-constructive. For this reason, it is common practice to state explicitly when the axiom is being used.

When Cantor was developing his theory of transfinite numbers, some of his results depended upon the Axiom of Choice. For example, the proof that the cardinality of the rational numbers is equal to the cardinality ${\aleph_0}$ of the natural numbers requires the axiom. Cantor was not aware of this.

It was Ernst Zermelo who, in 1904, formulated the axiom in a rigorous way. Zermelo explicitly stated the Axiom of Choice, introducing it as an assumption required for his proof that every set can be well-ordered. After that, it became apparent that there are numerous alternative formulations, all equivalent. That is, assuming any of these alternatives to be true, the others are automatically true.

Some of the equivalents of the Axiom of Choice (there are many more) are:

The Axiom of Choice.
The Hausdorff Maximality Principle.
The Well-ordering Principle.
Zorn’s Lemma.

The axiom of choice seems to be reasonable and most people accept it without difficulty. However, the well-ordering principle states that every set can be well-ordered in such a way that every subset has a least element. If you try this for the set of real numbers, you will soon realise that it is far from obvious. Furthermore, if the axiom of choice is true, some extraordinary results follow, for example, the Banach-Tarski paradox [ThatsMaths].

We finish with an amusing characterisation of AoC that depends upon the unreliability of intuition when it comes to infinite sets. Steven Krantz (2002) credits the following quotation to Jerry Bona:

The axiom of choice is obviously true,
the well-ordering principle obviously false,
and who can tell about Zorn’s lemma?

As observed in the Wikipedia article on AoC, this is a joke: although the three axioms are mathematically equivalent, the axiom of choice fits with our intuition, the well-ordering principle seems counter-intuitive, and Zorn’s lemma is so subtle that intuition provides little guidance.

We hope to return to this topic in a coming post, and look in more detail at the history of the axiom of choice and its equivalents.

Sources

${\bullet}$ Krantz, Steven G., 2002: The axiom of choice. Handbook of Logic and Proof Techniques for Computer Science, Springer, pp. 121-126.

${\bullet}$ That’s Maths, 2013: The Loaves and the Fishes. Link.

${\bullet}$ Wikipedia article Axiom of Choice: http://www.wikipedia.org/

Related

Published by thatsmaths