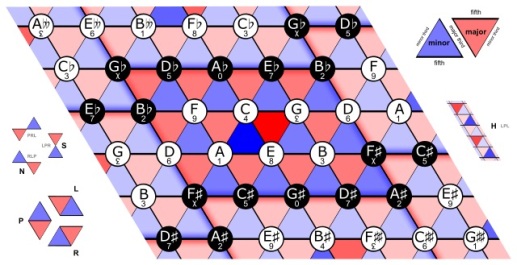
The circle of fifths is a remarkably useful diagram for the analysis of music. It shows the twelve notes of the chromatic scale arranged in a circle, with notes that are harmonically related (like C and G) being close together and notes that are discordant (like C and C♯) more distant from each other.
The Circle of Fifths
The twelve notes of the chromatic scale can be built up, starting from a base note called the tonic, by repeatedly scaling by 3/2. We treat notes differing by a power of 2 as if they were the same. This assumption of octave equivalence separates all notes into pitch classes, which we denote by the usual letters A to G.
Scaling by 3/2 twelve times gives a factor of 129.75, which is close to 128 = 27. The approximation 312 = 219 involving a small error (the Pythagorean comma) is called enharmonic equivalence. Thus, we do not distinguish between, for example, C♯ and Db, so that the scaling process is periodic, repeating after twelve iterations to give the circle of fifths.
The Tonnetz
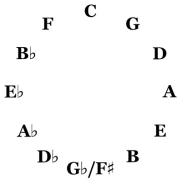
The Tonnetz (German for tone network) is a two-dimensional lattice diagram showing the harmonic relationships between chords. The idea originated with Leonhard Euler, who introduced a diagram of this sort in his book Tentamen novae theoriae musicae, published in 1739.
The Tonnetz is a very convenient tool for understanding the relationships between musical chords. It can be used to analyse chord progressions, to find relative major and minor keys, to transpose chord sequences and even to assist in the composition of innovative forms of music.
The Tonnetz starts from an unrolled circle of fifths. Each note is followed by the pure fifth above it and preceded by the fifth below it. Thus, C is preceded by F and followed by G:
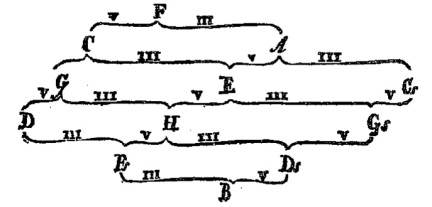
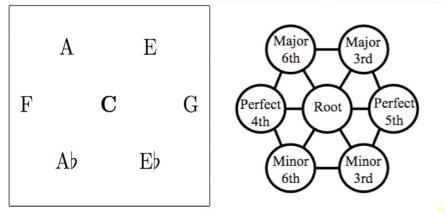
To this row is added another row above, shifted such that the two notes closest to any tone are a major third above it and a minor third below it. So, to the north-east of C is E, to the north-west is A:
When another row is added below, the following scheme results, showing all the triads involving the notes in the centre row:
Additional rows are added, either above or below, in precisely the same manner. Finally, we obtain a diagram that is periodic in both the horizontal and vertical directions. Harmonic affinity corresponds to distance on the Tonnetz diagram: the most harmonically consonant chords appear close together, the most distantly related chords are more remote.
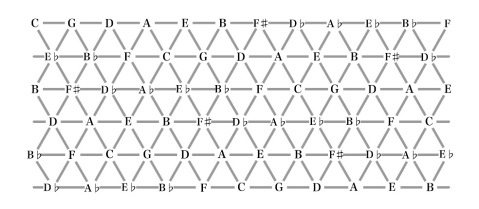
The diagram below shows the notes surrounding C. The intervals from the root (C) to the six surrounding notes are shown. The six triangles are the six triads that include C.
Twelve Tones and Modulo 12
The twelve tones of the chromatic scale can be represented by the integers from 0 to 11. Then modulo 12 arithmetic corresponds to enharmonic equivalence. We may choose 0 to represent C. The entire Tonnetz diagram can be written in numerical form:
We see that the numbers appearing at the left and right edges are the same. Moreover, the top and bottom rows are identical.
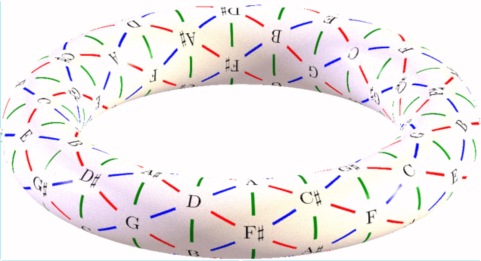
The diagram is periodic in two directions. It may be folded into a cylinder by joining the two vertical edges, giving a stack of circles-of-fifths. But it may then be folded again, joining the top to the bottom, to form a torus. Thus, the Tonnetz is topologically equivalent to a torus or doughnut, the cartesian product of two circles.
ThatsMaths 