“Typus Arithmeticae” is a woodcut from the book Margarita Philosophica by Gregor Reisch of Freiburg, published in 1503. In the centre of the figure stands Arithmetica, the muse of mathematics. She is watching a competition between the Roman mathematician Boethius and the great Pythagoras. Boethius is crunching out a calculation using Hindu-Arabic numerals, while Pythagoras uses a counting board or abacus (tabula) and – presumably – a less convenient number system. Arithmetica is looking with favour towards Boethius. He smiles smugly while Pythagoras is looking decidedly glum.
The figure aims to show the superiority of the Hindu-Arabic number system over the older Greek and Roman number systems. Of course, it is completely anachronistic: Pythagoras flourished around 500 BC and Boethius around AD 500, while the Hindu-Arabic numbers did not arrive in Europe until after AD 1200.
Fibonacci Brings New Numbers from Africa
A medieval mathematician, Leonardo of Pisa, usually known as Fibonacci, published a book, Liber Abaci (The Book of the Abacus) in 1202. While working in North Africa, he had come upon the decimal system of notation used by Arab mathematicians, and he introduced it to Europe in this book. In the same publication, while studying the way in which rabbit numbers increase, he described the famous sequence of numbers that bears his name.
The system introduced by Fibonacci is now called the Hindu-Arabic system, as it originated in India and came to Europe via the Arab world. It gradually supplanted the cumbersome system of Roman numerals.
MDCLXVI = 1666
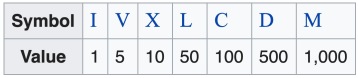
The Roman number system used letters for powers of 10 and multiples of these powers by 5. Thus, I, V, X, L, C, D and M stood for 1, 5, 10, 50, 100, 500 and 1000. Writing these in descending order we get MDCLXVI, which amounts to 1666. The year 1666 was a year of plague and of the Great Fire of London. It was also the year when Isaac Newton had some of his most brilliant ideas, and is often described as his annus mirabilis.
The Roman number system is too well known to require description here. We just recall that the notation can be additive, as with 7 = VII, or subtractive, as with 19 = XIX. Many clock designs mix these conventions, writing IIII for 4 and IX for 9. The Roman system was cumbersome and posed a serious obstacle to calculations. Computation with the abacus was quite common and, to some extent, overcame the difficulties of calculation with pen and paper (or stylus and slate). But the system certainly delayed progress in mathematics for many centuries. The transition from the Roman number scheme to the Hindu-Arabic numerals was surprisingly slow. For several centuries, there was rivalry between the abacists who used the old methods and the algorists who used the new numbers. This is the struggle depicted by Gregor Reisch in his woodcut. It was not until the sixteenth century that the Hindu-Arabic numerals became dominant.
Calculating with Roman Numerals
The simplest way to find the product of two numbers expressed as Roman numerals is the following:
-
Convert the two numbers to Hindu-Arabic form
-
Multiply them in the usual way
-
Convert the product back to a Roman numeral.
Of course, this algorithm was not available to the ancient Romans. They had no knowledge of the Hindu-Arabic system so familiar to us today. So they had to crunch out the product by brute-force methods.
Let us consider a problem of calculating with Roman numerals: what is LXXXVI multiplied by XLI? We change to additive notation and consider LXXXVI by XXXXI. Take the product of each “letter” in the first number by each in the second, using a multiplication table such as that shown below. Finally, add all the products and compress them using replacements such as IIIII = V and introducing subtractive notation if required.
Roman accountants and book-keepers had various tables to help them, but it was still a cumbersome process. With the Hindu-Arabic numerals to hand, there is an easier way: we convert the two numbers to the “decimal domain”, LXXXVI = 86 and XLI = 41. Then we multiply to get 3526 and convert this back to the “Roman domain” to get MMMDXXVI. But this is as anachronistic as the woodcut.
The Roman Abacus
The Ancient Romans developed a portable abacus, similar to but smaller than earlier ones used by the Greeks and Babylonians. It was an essential calculating aid for engineers, merchants, surveyors and tax collectors. It reduced the time required for basic arithmetic calculations. using Roman numerals.
A replica of a Roman hand abacus from 1st century AD is depicted here. It is believed that abacus devices were used in Babylonia as early as 2400 BC. The word abacus is a Latin word that, in turn, comes from the Greek αβακας (board or table). Pebbles were often used as counters on the abacus board and the Latin calculus for pebble has entered the mathematical lexicon.
ThatsMaths 