Al Biruni and the Size of the Earth

Abu Rayhan al-Biruni (AD 973–1048)

Al Biruni at Persian Scholars Pavilion in Vienna.

The 11th century Persian mathematician Abu Rayhan al-Biruni used simple trigonometric results to estimate the radius and circumference of the Earth. His estimate has been quoted as 6,340 km, which is within 1% of the mean radius of 6,371 km. While al-Biruni’s method was brilliant and, for its era, spectacular, the accuracy claimed must be regarded with suspicion.

Al-Biruni assumed that the Earth is a perfect sphere of (unknown) radius ${a}$ . He realised that because of the Earth’s curvature the horizon, as viewed from a mountain-top, would appear to be below the horizontal direction. This direction is easily obtained as being orthogonal to the vertical, which is indicated by a plumb line.

Al-Biruni located a suitable mountain in what is now Pakistan. He ascertained the height ${h}$ of the mountain above the surrounding level ground, and then measured the declination or dip angle ${\delta}$ of the horizon below the horizontal direction.

Measuring the Height of a Mountain

The unknown height ${h}$ is the length OM from a base level to the mountain peak. The simple but naive way to estimate the mountain height ${h}$ is to measure the angle of elevation ${\alpha}$ of the mountain top M from a point A at distance ${\ell}$ from the mountain (see Figure). Of course, this requires accurate knowledge of ${\ell}$ , the distance between point A and point O, which is impossible, since O is beneath the mountain.

Al-Biruni’s method of measuring the height of a mountain.

Al-Biruni’s clever strategy was to measure the elevation angles ${\alpha}$ and ${\beta}$ from two points ${A}$ and ${B}$ at different distances from the mountain. He measured the angle ${\alpha}$ by using an astrolabe to sight to the peak. He then moved further away to point B and measured the elevation angle ${\beta}$ at B. Since ${A}$ and ${B}$ were both on level ground, the distance ${d}$ between them could be measured with good accuracy. From the three quantities ${\{\alpha, \beta, d\}}$ , al-Biruni could then deduce the height ${h}$ using simple trigonometry.

Considering the right-angled triangle OMA, the mountain height ${h}$ and the (unknown) slope height ${s}$ are related by

$\displaystyle h = s \sin\alpha \,. \ \ \ \ \ (1)$

Considering angles in triangle AMB, we easily see that ${\gamma = \alpha - \beta}$ . Then, applying the sine rule to AMB, we get

$\displaystyle \frac{s}{\sin\beta} = \frac{d}{\sin(\alpha-\beta)} \,. \ \ \ \ \ (2)$

Combining (1) and (2), we easily conclude that

$\displaystyle h = \left(\frac{\sin\alpha\sin\beta}{\sin(\alpha-\beta)}\right) d = \left(\frac{\tan\alpha\tan\beta}{\tan\alpha-\tan\beta}\right) d \,. \ \ \ \ \ (3)$

This is the relationship that Al Biruni used to calculate the height of the mountain. The input values ${\{\alpha, \beta, d \}}$ can all be obtained with good precision so that, provided the tangents of angles can be evaluated accurately, an excellent estimate of the height ${h}$ can be made. Indeed, (3) has been used in surveying up to the present day.

Radius of the Earth

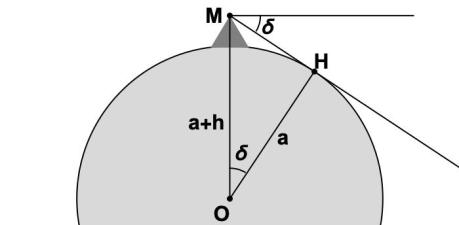
We now describe how al-Biruni used the mountain height to estimate the size of the Earth. The single additional measurement he required was the dip angle ${\delta}$ of the horizon as viewed from the mountain top (M in the figure below). It is clear that the angle MOH is equal to ${\delta}$ . It is also clear from the figure that ${\cos\delta = a/(a+h)}$ . This implies

$\displaystyle a = \frac{\cos\delta}{1-\cos\delta} h \ \ \ \ \ (4)$

which gives us a formula for Earth radius ${a}$ . Provided that he could evaluate the cosine of a small angle ${\delta}$ , al-Biruni could use this formula to obtain ${a}$ from ${h}$ and ${\delta}$ .

Al Biruni’s method of measuring the radius of the Earth.

Accuracy

It is often stated that al-Biruni’s estimate was within 1% of the correct value. This seems highly dubious, given that optical refraction was unknown to him and he made no allowance for it. Moreover, even in the absence of refraction, an evaluation of ${a}$ from (4) would have been problematical. Colman (2011) argued that, to obtain a value accurate to 1% using this equation, the cosine of the small angle ${\delta}$ must be accurate to six or more decimal digits. It seems unlikely that al-Biruni would have had values of this precision.

Colman (2011) proposed that, to evaluate the cosine of a small angle, al-Biruni might have used the half-angle formula in the form

$\displaystyle \cos\gamma = \sqrt{\frac{1+\cos 2\gamma}{2}}$

Starting with the exactly known value ${\cos 2\gamma=\cos 90^\circ = 0}$ , we successively halve the angle seven times to arrive at ${\cos 0.7^\circ \approx 0.999,925}$ . Al-Biruni could have measured the dip angle from several heights until he found a value of ${\delta=0.7^\circ}$ . Then he could evaluate ${a}$ using (4) with the accurate value of the cosine. But this, while possible, is speculative.

To get an appreciation of the order-of-magnitude of ${a}$ , we can approximate (4) by using the Taylor series expansion of ${\cos\delta}$ and keeping only the leading terms. This gives

$\displaystyle a = \frac{\cos\delta}{1-\cos\delta} h = \frac{1 + O(\delta^2)} { {\delta^2}/{2} + O(\delta^4) } h \approx \frac{2h}{\delta^2} \ \ \ \ \ (5)$

Using reasonable values of ${h = 1000\,}$ m and ${\delta = 1^\circ}$ , this gives ${a \approx 6,566\,}$ km and circumference ${C \approx 41,250\,}$ km, which is in the neighbourhood of the correct value.

Another method for the Mountain Height

Method used by Al-Biruni to measure the height of a mountain, as described in Al-Khalili (2012).

Jim Al-Khalili, in his book “Pathfinders: the Golden Age of Arabic Science”, describes an alternative method used by al-Biruni to measure mountain height. He uses a square board or frame of edge-length one cubit, or about 0.5 metre, lines up one edge (BC in the figure above) with the mountain peak E, and marks the corresponding line from corner D to E. Then geometric reasoning based on similar triangles allows him to deduce the mountain height FE.

Al-Khalili writes that al-Biruni was able to make a careful measurement of the distance AG. But a rough estimate for the angle ADG is ${s/d}$ where ${s}$ is the edge of the square and ${d}$ is the distance to the mountain. If ${s=0.5\,}$ m and ${d=3,000\,}$ m, we have ADG ${\approx 1/6,000}$ and AG ${\approx 1/12,000\,}$ m. Thus, it is required to measure a length of less than a tenth of a millimetre.

Sources

${\bullet}$ Al-Khalili, Jim, 2012: Pathfinders: the Golden Age of Arabic Science. Penguin Books, 302pp. ISBN: 978-0-1410-3836-0.

${\bullet}$ Colman, W. J. A., 2011: Measuring the radius of the Earth. Math. Gazette, 95, 532, 72–76.

${\bullet}$ Wikipedia article Al-Biruni: http://www.wikipedia.org/

* * * * *

That’s Maths II: A Ton of Wonders

by Peter Lynch now available.
Full details and links to suppliers at
http://logicpress.ie/2020-3/

>> Review in The Irish Times <<

* * * * *

ThatsMaths